4074. Найти
медиану - 2
Медиана играет
важную роль в мире статистики. По определению это число, которое делит массив
на две равные части. В этой задаче Вам необходимо найти значение медианы для
текущего набора целых чисел.
Например,
рассмотрим последовательность {1, 3, 6, 2, 7}.
Число 3 является медианой, так как по обе стороны от него находится в
точности по два целых числа: {1, 2} и {6, 7}.
Если
последовательность содержит четное количество чисел, как например
{1, 3, 6,2, 7, 8}, то одно число не может разбить массив на
две равные части, поэтому в качестве медианы будем рассматривать среднее
арифметическое центральных чисел {3,6}. То есть медиана равна (3 + 6)
/ 2 = 4.5. В задаче Вам следует выводить только целую часть
медианы, без дробной. То есть для данного примера ответом будет 4.
Вход. Состоит
из набора целых чисел x (0 ≤ x < 231),
их количество не более 106.
Выход. Для
каждого входного числа в отдельной строке вывести медиану текущей
последовательности. Для каждого значения медианы выводить только ее целую
часть.
|
Пример входа |
Пример выхода |
|
1 3 4 60 70 50 2 |
1 2 3 3 4 27 4 |
РЕШЕНИЕ
структуры
данных – куча
Анализ алгоритма
Промоделируем
решение задачи при помощи линейного массива. На каждом шаге будем хранить в нем
поступившие числа в отсортированном виде. Позицию, куда необходимо вставлять
новый элемент, ищем при помощи бинарного поиска. Однако вставка нового элемента
(например если массив содержится в структуре данных vector) при помощи метода insert происходит за линейное время.
Общее решение со временем O(n2) не пройдет по времени.
Объявим две кучи:
одна будет поддерживать минимум (min-куча), а вторая максимум (max-куча).
Работу куч будем моделировать таким образом, чтобы:
·
любой элемент max-кучи был меньше
любого элемента min-кучи (меньшие числа хранятся в max-куче, а
большие в min-куче);
·
размеры куч были одинаковы. В случае
нечетного количества элементов min-куча содержит на один элемент больше,
чем max-куча.
При поступлении
нового элемента заносим его в min-кучу, если он не меньше наименьшего элемента
min-кучи. Иначе заносим его в max-кучу. После чего балансируем
кучи так, чтобы сохранялось приведенное выше свойство их размеров.
·
Если размер max-кучи
больше размера min-кучи, то наибольший
элемент max-кучи переносим в min-кучу.
·
Если размер min-кучи
более чем на один элемент превышает размер max-кучи, то наименьший элемент min-кучи переносим
в max-кучу.
Медианой текущей
последовательности будет:
·
наименьший элемент min-кучи, если
количество чисел нечетно;
·
среднее арифметическое наименьшего
элемента min-кучи и наибольшего элемента max-кучи, если
количество чисел четно.
Вставка элемента
в кучу и балансировка происходит за время O(log2n). Общее
время работы алгоритма составит O(n log2n).
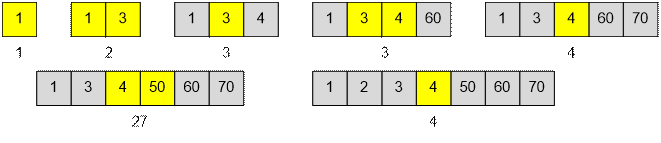
Пример
Рассмотрим
процесс вычисления медианы с поступлением чисел. Для удобства при поступлении
следующего числа мы сортируем последовательность. Под каждой
последовательностью приведено значение медианы.
После обработки
всех элементов примера состояние куч будет следующим:
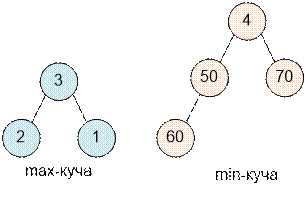
Поскольку
количество элементов нечетно, то медиана равна наименьшему элементу min-кучи,
то есть 4.
Пусть следующим
элементом будет 35. Поскольку он не меньше минимального элемента min-кучи,
то заносим его в min-кучу. Размер min-кучи на 2 больше размера max-кучи. Следует провести
балансировку: наименьший элемент min-кучи
(4) переносим в max-кучу. То есть удаляем 4 из min-кучи и
добавляем в max-кучу.
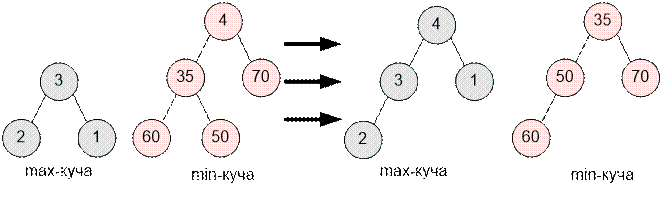
Теперь общее количество элементов в массиве четно, поэтому
медиана равна среднему арифметическому наименьшего элемента min-кучи
(35) и наибольшего элемента max-кучи (4), то есть (35 + 4) / 2 = 19 (в задаче
следует выводить только целую часть медианы).
Реализация
алгоритма
Объявим min-кучу
mMinHeap и max-кучу
mMaxHeap.
priority_queue<int, vector<int>,
greater<int> > mMinHeap;
priority_queue<int, vector<int>,
less<int> > mMaxHeap;
Инициализируем кучи. В переменной c подсчитываем
количество поступивших на вход чисел. Инициализируем кучи фиктивными
элементами.
mMaxHeap.push(-MAX);
mMinHeap.push(MAX);
c
= 1;
Обрабатываем очередное число.
while(scanf("%d",&n) == 1)
{
В зависимости от значения n
заносим его в одну из куч.
if (n >=
mMinHeap.top()) mMinHeap.push(n);
else
mMaxHeap.push(n);
Если размер max-кучи больше
размера min-кучи или размер min-кучи более чем на один элемент
превышает размер max-кучи, то проводим их балансировку.
if(mMaxHeap.size()
> mMinHeap.size())
{
Наибольший элемент max-кучи
переносим в min-кучу.
mMinHeap.push(mMaxHeap.top());
mMaxHeap.pop();
} else
if(mMaxHeap.size()
+ 1 < mMinHeap.size())
{
Наименьший элемент min-кучи
переносим в max-кучу.
mMaxHeap.push(mMinHeap.top());
mMinHeap.pop();
}
В зависимости от четности
количества элементов в массиве выводим значение медианы.
if (c % 2)
printf("%d\n",mMinHeap.top());
else printf("%d\n",(mMinHeap.top() +
mMaxHeap.top())/2);
c++;
}
Реализация
алгоритма - мультимножество
Это решение
работает значительно дольше предыдущего и может не проходить по времени. Однако
мы опишем его идею.
Последовательность
чисел храним в мультимножестве, итератор iter
указывает на медиану. Если множество содержит четное количество чисел, то
медианой является число ((*iter) + *(iter + 1)) / 2 (напомним, что в
языке Си с итераторами возможны лишь операции -- и ++, операция iter + 1 невозможна). Для вычисления
указанного выражения следует воспользоваться вторым итератором.
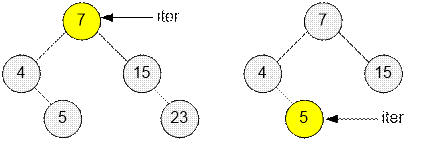
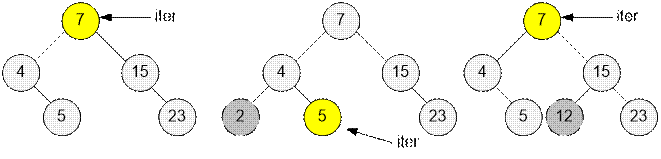
Пусть
мультимножество содержит нечетное количество чисел. Если вставка происходит
слева от итератора, то итератор следует сдвинуть на одну позицию влево. Если
вставка происходит справа от итератора, то итератор не изменяет своего
положения.
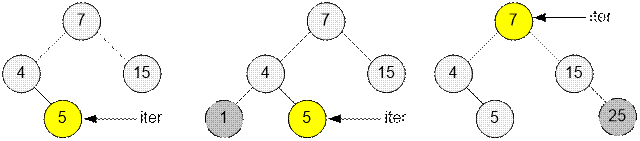
Пусть
мультимножество содержит четное количество чисел. Если вставка происходит слева
от итератора, то итератор не изменяет своего положения. Если вставка происходит
справа от итератора, то итератор следует сдвинуть на одну позицию вправо.
#include <cstdio>
#include <set>
using namespace std;
int
n, size;
multiset<int> s;
multiset<int>::iterator iter, iter1;
int
main(void)
{
scanf("%d",&n);
s.insert(n); iter = s.begin();
printf("%d\n",n);
size = 1;
while(scanf("%d",&n) == 1)
{
s.insert(n); size++;
if ((n <
*iter) && (size % 2 == 0)) iter--;
if ((n
>= *iter) && (size % 2 == 1)) iter++;
if (size
& 1) printf("%d\n",*iter);
else
{
iter1 = iter; iter1++;
printf("%d\n",(*iter
+ *iter1)/2);
}
}
return 0;
}